로또번호와 카오스이론

개요

로또번호를 추측해 볼 수 있을까?

로또번호를 추측하기 위한 많은 이론들이 나왔지만 그 중 유명한 카오스 이론에 대해 알아보고

파이썬을 통해 진짜 그런지 직접 돌려보겠다.

 

카오스 이론

카오스 이론이란 로또 당첨번호로 1,2,3,4,5,6 또는 2,4,6,8,10,12 또는 1,3,5,7,9,11 또는 전부 짝수가 되거나 전부 홀수가 되는 배열들과 같이 규칙을 가진 번호는 나오기 어렵다는 이론이다.

그래서 규칙을 가지는 번호는 전부 제하고 로또를 사서 당첨되고자 하는게 이 이론의 핵심이다.

 

과연 그럴까?

 

파이썬을 통해 규칙적인 번호로 추첨했을 때와 그렇지 않을때 각각 당첨확률이 어떻게 되는지 한번 확인해 보겠다.

각각 총 100번의 당첨이 될 때까지 연산하고, 당첨의 평균을 비교해보도록 하겠다.

 

추첨해보기

아래는 100번 추첨해보고 나온 확률의 평균을 비교하기 위해 작성한 파이썬 코드

import random
import time

pick_array = []
for i in range(6):
    pick_array.append(int(input("로또 번호 입력 : ")))
print("입력 된 로또 번호 : "+str(pick_array))
time.sleep(1)

try_for_win=[]

for i in range(100):
    try_num = 0
    while True:
        try_num += 1
        lotto_numbers = random.sample(range(1,46),6)
        sorted_lotto_numbers = sorted(lotto_numbers)
        if pick_array == sorted_lotto_numbers:
            break
        else:
            print(str(try_num)+"회차 당첨번호 : "+str(sorted_lotto_numbers))

    print(str(try_num)+"번째에 당첨")
    try_for_win.append(try_num)

average = 0
for win_num in try_for_win:
    win_rate = (1/win_num)*100
    average += win_rate
print(str(pick_array)+"의 평균 당첨 확률 : "+str(average/100))

 

 

결과

1,2,3,4,5,6로 추첨했을 때의 평균 확률

 

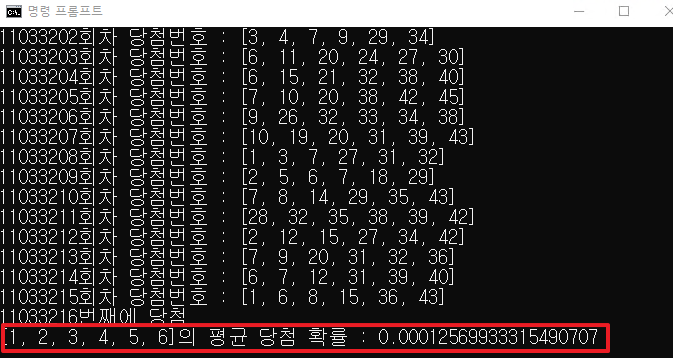
1,5,6,12,32,41로 추첨했을 때의 평균 확률

 

결과는 무작위로 선정한 번호보다 규칙적으로 선정한 번호 1,2,3,4,5,6이 당첨될 확률이 높았다. ㅋㄷㅋㄷ

 

결론

로또는 그냥 자동으로 돌리자

 

여담

로또 당첨 확률은 20키로짜리 쌀포대 11개에서 하나의 쌀알을 뽑는 것과 같은 확률이라고 한다.